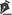POR QUE CALCULAR UM VALOR-P?

Considere um experimento no qual 10 indivíduos recebem um placebo e outros 10 recebem um diurético experimental. Após 8 h, a média do débito urinário no grupo placebo é de 769 ml versus 814 ml no grupo diurético - uma diferença de 45 ml (Figura 1). Como sabemos se essa diferença significa que a droga funciona e não é simplesmente resultado do acaso?



A forma mais comum de se abordar esse problema é utilizar um teste de hipótese. Primeiramente, estabelecemos a hi-pótese nula de nenhuma diferença estatística entre os grupos e a hipótese alternativa de uma diferença estatística. Em seguida, selecionamos um teste estatístico para computar uma estatística de teste, que é uma medida numérica padroni-zada da diferença entre os grupos. Sob a hipótese nula, esperamos que o valor da estatística de teste seja pequeno, mas há uma pequena probabilidade que essa seja grande, somente por acaso. Uma vez calculada a estatística de teste, a utilizamos para calcular o valor-p.

O valor-p é definido como a probabilidade de se observar um valor da estatística de teste maior ou igual ao encontra-do. Tradicionalmente, o valor de corte para rejeitar a hipótese nula é de 0,05, o que significa que, quando não há nenhu-ma diferença, um valor tão extremo para a estatística de teste é esperado em menos de 5% das vezes.

Agora voltemos ao nosso caso: estamos comparando médias e assumindo que os dados são distribuídos normalmente; por isso, usamos um teste t e computamos uma estatística t de 2,34, com um valor-p = 0,031. Como utilizamos um valor de corte de 0,05 para o valor-p, rejeitamos a hipótese nula e concluímos que existe uma diferença estatisticamente signi-ficativa entre os grupos. Então, o que "p = 0,031" significa? Significa que há apenas uma probabilidade de 3% de se observar uma diferença de 45 ml na média do débito urinário entre os grupos sob a hipótese nula. Como essa probabili-dade é muito pequena, rejeitamos a hipótese nula. Isso não significa que a droga seja um diurético, nem que haja uma chance de 97% de a droga ser diurética.

CONCEPÇÕES ERRADAS SOBRE O VALOR-P

Significância clínica vs. estatística do tamanho do efeito

É um equívoco achar que um valor muito pequeno de p signifique que a diferença entre os grupos é altamente relevan-te. Ao olharmos para o valor-p isoladamente, nossa atenção é desviada do tamanho do efeito. No nosso exemplo, o valor-p é significativo, mas uma droga que aumente a produção de urina em 45 ml não tem relevância clínica.

Valor-p não significante

Outro equívoco é achar que se o valor-p for maior do que 5%, o novo tratamento não tem nenhum efeito. O valor-p in-dica a probabilidade de se observar uma diferença tão grande ou maior do que a que foi observada sob a hipótese nula. Mas se o novo tratamento tiver um efeito de tamanho menor, um estudo com uma pequena amostra pode não ter poder suficiente para detectá-lo.

Interpretação exagerada de valor-p não significante, próximo a 5%

Outro conceito equivocado é acreditar que, se o valor-p está próximo de 5%, há uma tendência de haver uma diferença entre os grupos. É inadequado interpretar um valor-p de, digamos, 0,06, como uma tendência de diferença. Um valor-p de 0,06 significa que existe uma probabilidade de 6% de se obter esse resultado por acaso quando o tratamento não tem nenhum efeito real. Como definimos o nível de significância de 5%, a hipótese nula não deve ser rejeitada.

Tamanho do efeito vs. valor-p

Muitos pesquisadores acreditam que o valor-p é o número mais importante a ser relatado. No entanto, devemos nos concentrar no tamanho do efeito. Evite relatar o valor-p isoladamente e, preferencialmente, relate os valores médios para cada grupo, a diferença, o intervalo de confiança de 95% e, então, o valor-p.

LEITURA RECOMENDADA

1. Glantz SA. Primer in Biostatistics, 5th ed. New York: McGraw-Hill; 2002.