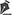Quando o objetivo de um pesquisador é avaliar a relação entre variáveis, análises de correlação e regressão são comumente usadas na ciência médica. Embora relacionadas, correlação e regressão não são sinônimos, e cada abordagem estatística é usada para uma finalidade específica e é baseada em um conjunto de suposições específicas.



Ao testar a correlação entre duas variáveis, utilizamos o coeficiente de correlação (r) para quantificar a força e a direção da relação entre duas variáveis numéricas, com resultados variando de −1 a 1. Quando r = 0, isso indica que não há uma relação linear entre as duas variáveis; quando r = 1, há uma perfeita relação positiva entre as duas variáveis, implicando que, à medida que o valor de uma variável aumenta, o valor da outra também aumenta (Figura 1). Quando r = −1, há uma relação negativa perfeita, implicando que, à medida que o valor de uma variável aumenta, o valor da outra diminui. Na maioria dos casos, a força da relação entre as variáveis não é perfeita; portanto, r não é exatamente 1 ou −1. A força de uma correlação é comumente interpretada como fraca (r < ±0,4), moderada (r variando de ±0,4 a ±0,7) e forte (r > ±0,7).(1) Por fim, destacamos que quando a correlação é usada como uma abordagem estatística, os dados devem ser derivados de uma amostra aleatória; as variáveis devem ser contínuas; os dados não devem incluir valores discrepantes; cada par de variáveis precisa ser independente(1); e a correlação não implica necessariamente uma relação de causa e efeito.

 






A regressão é indicada quando uma das variáveis é um desfecho e a outra é um potencial preditor desse desfecho, em uma relação de causa e efeito. Se o desfecho for uma variável contínua, é indicado um modelo de regressão linear e, se for binária, é utilizada uma regressão logística. A regressão também quantifica a direção e a força da relação entre duas variáveis numéricas, X (preditor) e Y (desfecho); no entanto, diferentemente da correlação, essas duas variáveis não são intercambiáveis, e a correta identificação do desfecho e do preditor é fundamental. Os modelos de regressão também permitem avaliar mais de uma variável preditora, outra diferença importante da análise de correlação.(2)



A regressão é um modelo matemático linear representado pela equação Y = β0 + β1X (Figura 1). Quando o valor de X (preditor) é zero, o valor de Y é β0 (intercepto de linha) e β1 é a inclinação, o que nos fornece informações sobre a magnitude e a direção da associação entre X e Y, de forma semelhante ao coeficiente de correlação. Quando β1 = 0, não há associação entre X e Y. Quando β1 > 0 ou β1 < 0, a associação entre X e Y é positiva ou negativa, respectivamente. Pressupostos importantes da regressão linear são normalidade e linearidade da variável desfecho, independência entre as duas variáveis e variância igual da variável desfecho ao longo da linha de regressão.(2)

Concluindo, ao avaliar a relação entre duas variáveis, precisamos entender as diferenças entre correlação e regressão e escolher qual teste estatístico é o melhor para responder à pergunta da pesquisa.



REFERÊNCIAS



1. Schober P, Boer C, Schwarte LA. Correlation Coefficients: Appropriate Use and Interpretation. Anesth Analg. 2018;126(5):1763-1768. http://doi:10.1213/ANE.0000000000002864

2. Kutner MH, Nachtsheim CJ, Neter J, Li W. Simple Linear Regression. In: Kutner MH, Nachtsheim CJ, Neter J, Li W. Applied linear statistical models. 5th ed. New York: McGraw-Hill; 2005. p. 1-87.